Ginormous Coincidences?
Analyzing Francesca Gino's attempted rebuttals of allegations against her research
In June, three academics - Uri Simonsohn, Leif Nelson and Joe Simmons - set off a firestorm when they released a series of four posts (1, 2, 3, 4) on their blog, Data Colada, “detailing evidence of fraud in four academic papers co-authored by Harvard Business School Professor Francesca Gino.”1 Following a parallel investigation at Harvard, Gino has been placed on administrative leave and Harvard requested the papers in question be retracted.2
Maintaining her innocence, Gino subsequently sued Harvard and Data Colada in Federal Court for defamation. On Friday, Gino launched a website attempting to rebut the allegations against her research, including analysis (and the promise of more) countering the claims made by Data Colada. Gino admits her critics “may sound compelling”, but claims their arguments are “incomplete and misleading.”
This post is not, per se, about the evidence of fraud presented by Data Colada. Rather it is an attempt to critically analyze the counterpoints that Gino is raising in her defense.
Double Down or Nothing
Before beginning, it is useful to consider as a completely abstract exercise the options available to an academic whose work is accused of being (correctly or not) either catastrophically wrong or fraudulent. Supposing they don’t wish to admit the criticisms are largely correct (whether taking responsibility or blaming others), broadly speaking the accused has the following options:
Full Rebuttal: Carefully show that all criticisms are either based on explicit errors, or that there are innocent explanations for all suspicious-seeming facts.
Partial Rebuttal: Find specific points on which the criticism oversteps or involves errors, rebut those, and treat this as undermining the aggregate accusations.
Muddy the Waters: Deny the accusations, and attempt to obfuscate and muddy the waters. Typically this may involve raising a lot of difficult-to-litigate technical detail - relatively few people (even amongst academics) will expend the effort required to determine if one party is definitively right once a dispute gets bogged down in interminable detail. Similar to criminal trials, creating reasonable doubt is generally sufficient to save someone’s reputation.
A truly innocent party will naturally prefer Option 1 to Option 2 and so forth. A party that is truly guilty (whether of fraud, or merely of screwing up) doesn’t have a tenable path to achieving Option 1, and will prefer Option 2 to Option 3 if both are feasible. Someone who attempts to muddy the waters is implicitly admitting that this is their best option, suggesting that the criticisms probably are valid. But probably can leave residual doubt, and furthermore, there’s no magic bullet to tell Options 1-3 apart. For example, sometimes the correct rebuttal requires large amounts of technical detail.
In my prior experience replicating sensational sounding academic claims, I’ve found that the more simply competing claims can be presented and evaluated, the easier it becomes for people to understand the merits of the accusations. And in turn, the more people who do so.
Hence this post.
Part 1 - “Clusterfake”
The remainder of this post discusses the accusations made by Data Colada in Part 1 of their series of posts on articles co-authored by Gino (for simplicity, I’m following their choice of titles). The paper in question is Shu, Mazar, Gino, Ariely, & Bazerman (2012), "Signing at the beginning makes ethics salient….", Proceedings of the National Academy of Sciences.
The paper claims that people are less likely to act dishonestly (while filling out a form) when they sign an honesty pledge at the top of a form (treatment condition 1) compared to at the bottom (treatment condition 2).
Data Colada’s Accusation:
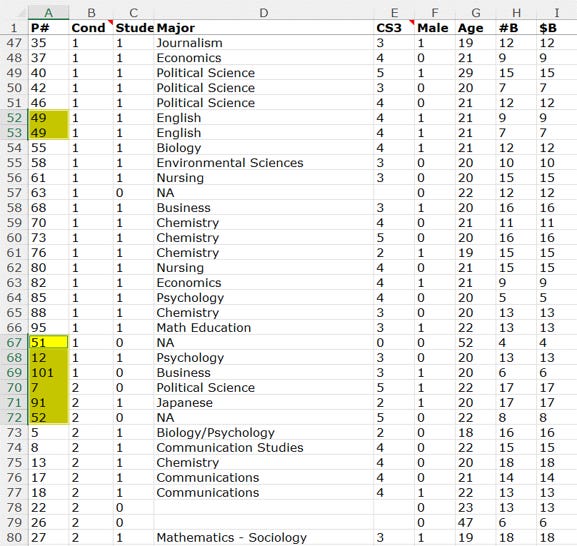
Data Colada - examining the data file used for the study - argue that the raw data strongly appears to have been manipulated. Specifically:
The data is almost perfectly sorted by Participant ID and study condition. But there is a block of six observations where the Participant IDs are out-of-sequence, suggesting they may have been manually moved.
One observation (Participant ID 49) appears to have been duplicated.
Suspiciously, these 8 observations have very extreme outcome values (see graph from Data Colada below). They provide the highest values in the sign-at-the-bottom group (higher predicted dishonesty) and amongst the lowest values in the sign-at-the-top group (lower predicted dishonesty). Collectively, they produce a huge net effect in the predicted direction.
If the 8 observations were unremarkable, and their erroneous position in the data file were innocuous, they should have typical:
Values within their treatment condition.
Average difference between treatment conditions.
Clearly they don’t. A natural - and Data Colada’s - inference is that the data file was manipulated, manually changing the recorded treatment condition of these observations (and then moving the rows to restore the sort order by treatment condition) to yield the hypothesized effect. For example, assigning observations with high (low) outcome levels to treatment condition 2 (1).
Data Colada then provide a second supporting strand of evidence - forensic file analysis using Excel’s CalcChain3 - that the six out-of-sequence observations were indeed manually moved.4
Gino’s Response:
Gino has responded to these accusations here.
Regarding the eight rows which Data Colada identify as suspicious, she argues:
Data Colada cherry-pick which duplicate and out-of-sequence observations to include.
Under a more consistent rule, two of the six rows that Data Colada identify as out-of-sequence, are in fact not so.
There are two additional out-of-sequence observations, and another two observations with duplicate IDs. Data Colada either fail to identify or include these in their analysis.5
The study has three experimental conditions (control (0), sign-at-the-top (1), sign-at-the-bottom (2)), but Data Colada cherry-pick in their analysis by excluding the control group.
Per Gino’s criteria, this gives ten observations that are either out-of-sequence or duplicates, but only six of these are in the observations flagged by Data Colada as suspicious.
Analyzing the resulting data using her classification, Gino argues:
There is no statistically significant difference between the three experimental groups for the ten flagged observations [F(2,9) = 3.28, p = .099]. (See graph by Gino below).
If the ten flagged observations are dropped, the findings of the original study still hold. She argues this removes any motive to manipulate the data: “Why would I manipulate data, if not to change the results of a study?”
Which Claims are Out of Order?
Let’s critically examine Gino’s claims.
Which Conditions to Examine?
The easiest argument to dispel with is whether it misleading cherry-picking for Data Colada to exclude the control group (experimental condition 0) and focus only on comparing the sign-at-the-bottom and sign-at-the-top treatment groups.
Simply put, no, it is not.
Suppose there are three conditions in a study: A, B and C, and the primary hypothesis is that B produces higher values of some outcome than C. The obvious place to commit fraud is in groups B and C, to ensure B yields higher results.6 Altering values in group A has no effect on the B vs C difference, and is thus approximately useless. The obvious way to test for fraud is to look in the places where fraud, if it exists, is most likely to be.
In this paper, the key question is whether signing-at-the-top yields more honesty than signing-at-the-bottom. It’s literally in the name of the paper. Data Colada’s focus on - and comparison of the suspicious data in these two groups - is perfectly appropriate.
This matters. Gino says there is no statistically significant difference between the three experimental groups for her (per her method) ten flagged observations [F(2,7) = 3.28, p = 0.099]. In fact, discussing whether the flagged observations show anything suspicious, she gallingly challenges the reader: “Look at the chart [above] and and try to find the pattern”. Er, about that… the sign-at-the-bottom group clearly has much higher values than the sign-at-the-top group. And indeed, the slightest additional data analysis confirms this. The very same regression that yields the F-statistic above which Gino cites as statistically insignificant shows that there is a significant (p = 0.04) difference between these two treatment groups for Gino’s ten flagged observations!7
Which Observations to Examine as Suspicious
Data Colada identify eight observations (in conditions 1 and 2) as suspicious. Gino claims they use an inconsistent approach, and a correct execution of their ‘rule’ would flag ten observations. Who is right?
The disagreement largely comes down to identifying which observations are out-of-sequence.
Gino proposes the following rule: “within each condition, an out-of-sequence observation is one where the ID is not in ascending order” (i.e. it instead follows a higher ID). She (as best I can tell) falsely ascribes this rule to Data Colada - they never describe their rule in this way.8 Having falsely described their procedure, she then accuses them of failing to follow their own rule correctly. She then uses this rule to construct her proposed set of out-of-sequence observations, although amusingly seems to make an error in doing so (see below).
To make this more tangible, consider the following example:
80, 86 and 4 (highlighted in red) are the only values here that follow a higher value, and thus are out-of-sequence under Gino’s definition. But it does not take a genius to see that a rather more plausible interpretation is that there is a jumble of observations {100, 80, …, 87} that have been incorrectly spliced into the numbers 1-10. Data Colada’s process would seem to sensibly flag the entire {100, 80, …, 87} jumble as out-of-sequence, while Gino’s rule would only flag a few observations erratically, including one (4) that should sensibly be decreed as in-sequence.
More generally, Gino’s rule makes very little sense. When dealing with the possibility of a block of consecutive out-of-sequence observations, within such a block it is of little relevance whether observation n+1 has a higher ID than observation n. Additionally, in a sequence like 1, 2, 3, 100, 4, 5 it identifies (erroneously) 4 (not 100) as the out-of-sequence observation.
With this in mind, let’s consider the actual values in question.
The first table below is what Data Colada shows, showing the observations in context. The second table, from Gino, lists only observations flagged by either party.9
Here are the key observations, listed in order (condition = 1 in red, condition = 2) in blue):
Data Colada observe this and concludes that the six observations from 51 to 52 are all out-of-sequence, while under Gino’s rule, only 51, 52, 12, and 5 follow higher valued IDs within the same condition and thus are deemed out-of-sequence. She also appears to erroneously categorize ID 91 as out-of-sequence, in violation of her stated rule.10
It is thus unsurprising that Gino’s rule captures a set of observations where the difference in outcomes between treatment condition 1 and 2 is less stark - the observations she considers aren’t the most plausibly manipulated ones. I too have failed to find Original Recipe Chicken at McDonalds.
The set of observations flagged by Data Colada is much more sensible. Gino’s argument that a different, weirdly defined, set of observations exhibit less suspicious patterns is very weak.
Results without Flagged Observations
Recall that Gino argues that if the ten observations she flags are dropped, the findings of the original study still hold, thus removing any motive for manipulation. Since her set of flagged observations makes little sense, this is presumptively irrelevant.
But supposing my previous argument was wrong, does this contention have merit? There are at least two problems with her claim:
Recall that Gino argues there is no statistically significant difference between the three experimental groups for the ten observations she flags. In doing so, she cites only the results of a joint F-test, with a p-value of p = 0.099. Yet, the same joint F-test for whether the outcome varies across conditions when dropping the flagged observations has a p-value of p = 0.057. Whatever one thinks of arbitrary p-value thresholds, by traditional interpretation this result is not statistically significant either, yet Gino claims otherwise.11 Who exactly is cherry-picking here?
If, as conjectured by Data Colada, the treatment condition of observations has been switched, the manipulation is not fully ‘undone’ by dropping the suspect observations. Suppose observations with low outcome values are switched from condition 1 to condition 2. Dropping these observations still leaves the mean outcome for condition 1 artificially higher. A significant result remaining after dropping these observations does not imply the result already held before any claimed manipulation. Yet this is necessary for the claimed reduced motive for such manipulation to be credible.12
Summary
Gino argues that Data Colada misleadingly excludes the control group from their analysis of whether the observations they flag exhibit suspicious patterns. This claim is baseless. The difference in outcomes between the sign-at-the-bottom and sign-at-the-top treatments is the main focus of the paper, and the obvious place to test for fraud.
Gino argues that Data Colada cherry-pick which observations they flag as suspicious, and don’t consistently follow their own stated criteria. Yet the criteria she lists is seemingly her own, not Data Colada’s, and makes little sense. Data Colada appear to make the most obvious choices regarding which observations to flag as suspicious.
Even using Gino’s set of ten observations, there is a strikingly large statistically significant difference in the claimed expenses outcome between the top and bottom treatments.
It is essentially irrelevant that some of the results remain after dropping the flagged observations, because this does not imply the result already held before any claimed manipulation.
A disclosure: I got my PhD in Business Economics from HBS in 2022. I imagine I was in the same room as Gino multiple times, but I can’t recall ever interacting with her.
Strictly speaking, one had already been retracted based on separate concerns regarding data fabrication.
Apparently the CalcChain analysis is only feasible because new variables are created with formulas within the .xlsx file. The 1980s called, they want their data management practices back.
Of course, there is nothing fraudulent about moving rows about. According to Data Colada, this second strain of evidence matters because the data appears to have (previously) been sorted by the Condition and Participant ID variables. But these 6 observations appear to have different original positions in the sorted dataset. And to have previously been placed in such positions in the sorted dataset, they must have previously had different listed values of the Condition variable.
Data Colada flag as duplicate two observations that have identical IDs and demographics. Gino argues they are cherry-picking because they don’t also flag two observations that share an ID but have completely different demographics to each other. The chance of any two randomly chosen observations having identical demographics is very low, so contra Gino, the distinction between these cases are obvious, and this point merits no further attention.
Strictly speaking, there are all sorts of tricks a competent fraudster might undertake, to both produce the desired result and cover their tracks. But at no point here does Data Colada appear to be alleging the existence of competent fraud.
The p-value is lower again (p = 0.019) if the sample is restricted to the eight observations Gino flags in the two treatment groups. Separately, it appears both Gino and Data Colada calculate homoskedastic standard errors - perhaps due to the sample sizes involved. Heteroskedasticity robust standard errors yield similar or stronger results.
Rather, they appear to be using a ‘I know it when I see it’ procedure. A candidate formal definition? Assuming there is only k blocks of misordered data (for some given k), find the smallest set of jumbled observations that leaves all other observations correctly ordered.
The astute reader may note that Data Colada are providing far more information here - to evaluate Gino’s claims, one needs to look at Data Colada’s table.
So much for her claim that “Simple as this sounds, for some reason Data Colada misapplies its own rule, without any explanation.”
When dropping Gino’s flagged observations, there only remains a significant effect for the difference between the two treatment conditions. But by this exact criterion, as mentioned above there is also a statistically significant difference between the two treatment conditions amongst the ten flagged observations, which Gino conveniently never mentions.
Gino also complains that Data Colada distorts the evidence by selectively showing results only for one of the three outcome measures used in the paper (Claimed Expenses). In particular, she notes that main result still holds for the other outcome measures, irrespective of whether Data Colada’s eight or Gino’s ten flagged observations are dropped. But the exact same problem exists here - if manipulation exists, dropping flagged observations is insufficient. And notably, contrary to Gino’s claim that “analysis of the other two metrics fail to support [Data Colada’s] allegations” the results for these outcomes are strikingly weaker once the observations Data Colada flagged are dropped.







I'm a bit concerned by the suggestion that what one does is look at the most plausibly manipulated pieces of data.
Consider a perfectly honest study which reaches some desired statistically significant result. Since clearly no one would introduce fake data unless it moved the result from insignificant/non-existent to significant we can infer that looking at the subset of data most likely to have been manipulated always switches insignificant to significant results.
The test can't be what's the most plausible manipulated subset of the data but something a bit more complicated that considers how plausible/sus those data points happen to be.
> Suppose observations with low outcome values are switched from condition 1 to condition 2. Dropping these observations still leaves the mean outcome for condition 1 artificially lower.
This should say "artificially higher", right?